Nonlinear Problems in One Variable¶
What Is Not Possible¶
Solvers can only return an approximate answer or signal that no solution was found in the allotted time.
Exercise 1¶
[1]:
def Newtons_Method(f, f_prime, x_c):
return x_c - f(x_c) / f_prime(x_c)
f = lambda x: x**4 - 12 * x**3 + 47 * x**2 - 60 * x
f_prime = lambda x: 4 * x**3 - 36 * x**2 + 94 * x - 60
[2]:
x_c = 2
for i in range(5):
x = Newtons_Method(f, f_prime, x_c)
print('Iteration {0}: {1}'.format(i, x))
x_c = x
Iteration 0: 2.75
Iteration 1: 2.954884105960265
Iteration 2: 2.997853245312536
Iteration 3: 2.99999465016014
Iteration 4: 2.9999999999666165
[3]:
x_c = 1
for i in range(12):
x = Newtons_Method(f, f_prime, x_c)
print('Iteration {0}: {1}'.format(i, x))
x_c = x
Iteration 0: 13.0
Iteration 1: 10.578892912571133
Iteration 2: 8.78588342536825
Iteration 3: 7.469644320482534
Iteration 4: 6.517931578972248
Iteration 5: 5.848418791850394
Iteration 6: 5.4023336439265215
Iteration 7: 5.139173220737766
Iteration 8: 5.024562327545462
Iteration 9: 5.000967258633622
Iteration 10: 5.000001586728139
Iteration 11: 5.000000000004287
Exercise 2¶
On CDC machines, the base is 2 and the mantissa has 48 bits. The machine is accurate up to \(\log 2^{48} \sim \log 10^{14.4} \approx 14\) decimal digits.
Given \(x_k = 1 + 0.9^k\), \(x_k \rightarrow 1\) implies
Evidently, it will take \(\lceil k \rceil\) iterations to converge to \(1\) on a CDC machine. The convergence rate is given by
which shows that \(q\)-linear convergence with constant 0.9 is not satisfactory for general computational algorithms.
Exercise 3¶
The sequence \(x_k = 1 + 1 / k!\) converges \(q\)-superlinearly to one because
[4]:
import matplotlib.pyplot as plt
import numpy
f = lambda x: 1 + 1 / numpy.math.factorial(x)
x_star = 1
C = []
for i in range(1, 20):
x_k = f(i - 1)
x_kp1 = f(i)
C.append(abs(x_kp1 - x_star) / abs(x_k - x_star))
plt.plot(C)
plt.xlabel(r'Iteration $k$')
plt.ylabel('Convergence Rate')
plt.title(r'$1 + 1 / k! \rightarrow 1$')
plt.show()
<Figure size 640x480 with 1 Axes>
Exercise 5¶
Given \(\left\{ x_k \right\}\) has \(q\)-order at least \(p\) and \(e_k = |x_k - x_*|\), let \(b_k = |x_{k - 1} - x_*|\). By definition of \(q\)-order at least \(p\), \(\left\{ b_k \right\}\) converges to zero where \(e_k \leq b_k\) and \(\left| x_k - x_* \right| \leq c \left| x_{k - 1} - x_* \right|^p\) holds.
Applying L’Hopital’s rule to the following indeterminate form
demonstrates convergence to a finite value.
Exercise 7¶
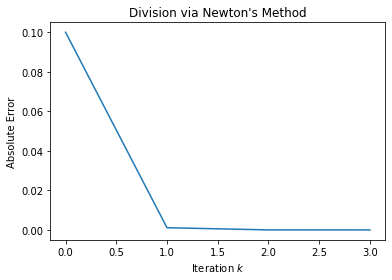
To reuse the framework of Newton’s method covered so far, we need to formulate a local model around \(f(x) = 1 / a\) such that we can solve for the root of the model.
Defining \(f(x) = a x - 1\) is perfectly valid and does not use any division operators. Unfortunately, this model still requires a division by \(f\) and \(f'\) for Newton’s method. To avoid those divisions, the model should be written as \(f(x) = 1 / x - a\) with \(f'(x) = -1 / x^2\).
The absolute error
indicates the convergence rate is \(q\)-quadratic.
[5]:
import matplotlib.pyplot as plt
a = 9
f = lambda x_c: x_c * (2 - a * x_c)
x_star = 1 / a
x_c = round(1 / a, 1)
C = [x_c]
for i in range(3):
x_k = f(x_c)
x_c = x_k
C.append(abs(x_k - x_star))
plt.plot(C)
plt.xlabel(r'Iteration $k$')
plt.ylabel('Absolute Error')
plt.title("Division via Newton's Method")
plt.show()
Exercise 8¶
Define \(D = \left| x_0 - z_0 \right|\) as the length of the interval around \(x_*\). The bisection method would stop once \(D \approx 0\). Since
and
the bisection method’s convergence rate is q-linear. Note that the bisection method does not extend naturally to higher dimensions.
[6]:
f = lambda x: 1 / x - 5
x_k, z_k = 0.1, 1
for i in range(12):
x_n = (x_k + z_k) / 2
if f(x_k) * f(x_n) < 0:
z_n = x_k
else:
z_n = z_k
x_k, z_k = x_n, z_n
print(x_n)
0.55
0.325
0.21250000000000002
0.15625
0.184375
0.19843750000000002
0.20546875000000003
0.201953125
0.2001953125
0.19931640625000002
0.199755859375
0.1999755859375
Exercise 9¶
The following analysis are based on Theorem 2.4.3.
[7]:
import matplotlib.pyplot as plt
import numpy
class HybridQuasiNewton:
def __init__(self, tau=None, typx=None):
self._kEpsilon = numpy.finfo(float).eps
self._kRootEpsilon = numpy.sqrt(self._kEpsilon)
#parameters to solver
self._tau = tau
if tau is None:
self._tau = (self._kRootEpsilon,) * 2
self._typx = typx
if typx is None:
self._typx = (1,)
self._secant_state = None
def evaluate_fdnewton(self, f, x_c):
#finite forward-difference
h_c = self._kRootEpsilon * max(abs(x_c), self._typx[0])
f_xc = f(x_c)
a_c = (f(x_c + h_c) - f_xc) / h_c
x_k = x_c - f_xc / a_c
x_n = self._backtracking_strategy(f, x_c, x_k)
return self._stop(f, x_c, x_n), x_n
def evaluate_newton(self, f, f_prime, x_c):
x_k = x_c - f(x_c) / f_prime(x_c)
x_n = self._backtracking_strategy(f, x_c, x_k)
return self._stop(f, x_c, x_n), x_n
def evaluate_secant(self, f, x_c):
if self._secant_state is None:
#secant method uses previous iteration's results
h_c = self._kRootEpsilon * max(abs(x_c), self._typx[0])
#compute finite central-difference
a_c = (f(x_c + h_c) - f(x_c - h_c)) / (2 * h_c)
f_xc = f(x_c)
x_k = x_c - f_xc / a_c
self._secant_state = (x_c, f_xc)
else:
x_m, f_xm = self._secant_state
f_xc = f(x_c)
a_c = (f_xm - f_xc) / (x_m - x_c)
x_k = x_c - f_xc / a_c
self._secant_state = (x_c, f_xc)
x_n = self._backtracking_strategy(f, x_c, x_k)
converged = self._stop(f, x_c, x_n)
if converged:
self._secant_state = None
return converged, x_n
def _backtracking_strategy(self, f, x_c, x_n):
while abs(f(x_n)) >= abs(f(x_c)):
x_n = (x_c + x_n) / 2
return x_n
def _stop(self, f, x_c, x_n):
return abs(f(x_n)) < self._tau[0] or\
abs(x_n - x_c) / max(abs(x_n), self._typx[0]) < self._tau[1]
def plot_convergent_sequence(solver, x_0, x_star):
x_c = x_0
seq = [abs(x_c - x_star)]
converged = False
k = 0
while not converged:
converged, x_n = solver(x_c)
x_c = x_n
seq.append(abs(x_c - x_star))
k += 1
_ = r'$x_0 = {0:.3f}, {1} = {2:.3f}, x_* = {3:.3f}$'
_ = _.format(x_0, 'x_{' + str(k) + '}', x_c, x_star)
p = plt.plot(range(len(seq)), seq,
label=_)
plt.legend()
plt.xlabel(r'Iteration $k$')
plt.ylabel('Absolute Error')
plt.title('Convergence Rate')
plt.show()
[8]:
hqn = HybridQuasiNewton()
f = lambda x: x**2 - 1
f_prime = lambda x: 2 * x
x_0 = 2
METHODS = ["Newton's Method",
"Finite-Difference",
'Secant Method']
STR_FMT = '{0!s:16}\t{1!s:16}\t{2!s:16}'
print(STR_FMT.format(*METHODS))
x_n = [x_0, ] * 3
converged = [False, ] * 3
while False in converged:
converged[0], x_n[0] = hqn.evaluate_newton(f, f_prime, x_n[0])
converged[1], x_n[1] = hqn.evaluate_fdnewton(f, x_n[1])
converged[2], x_n[2] = hqn.evaluate_secant(f, x_n[2])
print(STR_FMT.format(*x_n))
Newton's Method Finite-Difference Secant Method
1.25 1.2500000055879354 1.25
1.025 1.0250000022128225 1.0769230769230769
1.0003048780487804 1.0003048784367878 1.0082644628099173
1.0000000464611474 1.000000046464312 1.0003048780487804
1.000000000000001 1.0000000000000013 1.0000012544517356
1.0 1.0 1.0000000001911982
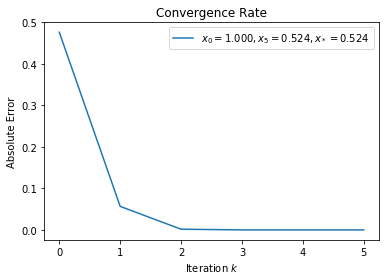
(a)¶
Newton’s method will converge \(q\)-quadratically given \(x_0 = 1\) because \(x_* \in [0, 1]\) and within that range, \(\exists \rho > 0\) such that \(\left| f'(x) \right| > \rho\).
[9]:
hqn = HybridQuasiNewton()
f = lambda x: numpy.sin(x) - numpy.cos(2 * x)
x_0 = 1
x_star = 0.523598775598
solver = lambda x: hqn.evaluate_secant(f, x)
plot_convergent_sequence(solver, x_0, x_star)
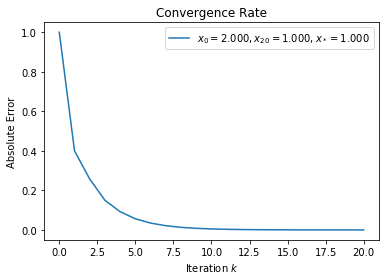
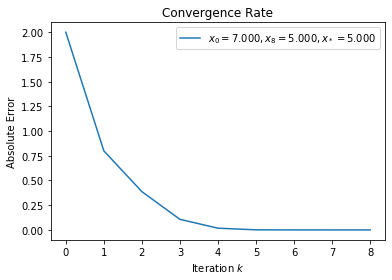
(b)¶
Newton’s method will converge \(q\)-quadratically to \(x_* = 5\) when \(x_0 = 7\). When \(x_0 = 2\), it will converge \(q\)-linearly to \(x_* = 1\) because \(f'(x_* = 1) = 0\) i.e. the multiple roots at \(x_*\) violate the \(\rho > 0\) condition.
[10]:
hqn = HybridQuasiNewton()
f = lambda x: x**3 - 7 * x**2 + 11 * x - 5
x_0 = 2
x_star = 1.00004066672
solver = lambda x: hqn.evaluate_secant(f, x)
plot_convergent_sequence(solver, x_0, x_star)
x_0 = 7
x_star = 5
plot_convergent_sequence(solver, x_0, x_star)
(c)¶
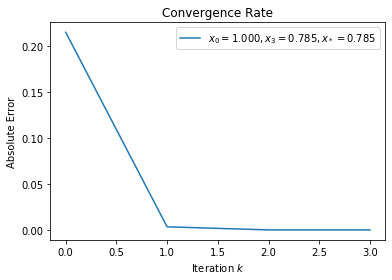
Newton’s method will converge \(q\)-quadratically when \(x_0 = 1\).
[11]:
hqn = HybridQuasiNewton()
f = lambda x: numpy.sin(x) - numpy.cos(x)
x_0 = 1
x_star = 0.78539816335
solver = lambda x: hqn.evaluate_secant(f, x)
plot_convergent_sequence(solver, x_0, x_star)
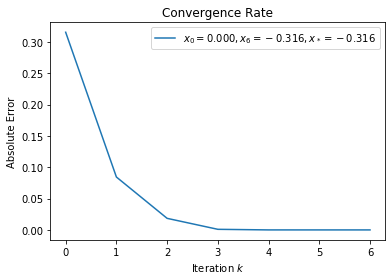
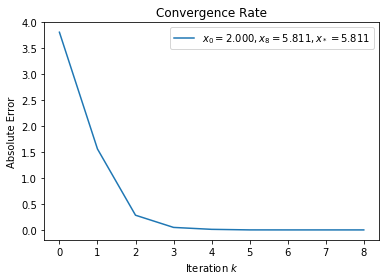
(d)¶
Both \(x_0 = 0\) and \(x_0 = 2\) will achieve \(q\)-quadratic convergence with Newton’s method. However, \(x_0 = 2\)’s convergence is slower than \(x_0 = 0\)’s because there are two zero crossings for \(f'(x)\) on the way to \(x_*\).
[12]:
hqn = HybridQuasiNewton()
f = lambda x: x**4 - 12 * x**3 + 47 * x**2 - 60 * x - 24
x_0 = 0
x_star = -0.315551843713
solver = lambda x: hqn.evaluate_secant(f, x)
plot_convergent_sequence(solver, x_0, x_star)
x_0 = 2
x_star = 5.81115950152
plot_convergent_sequence(solver, x_0, x_star)
Exercise 10¶
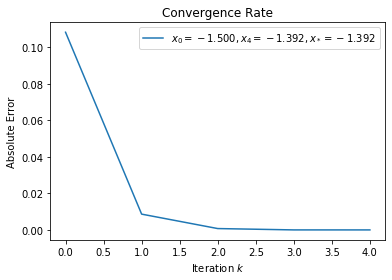
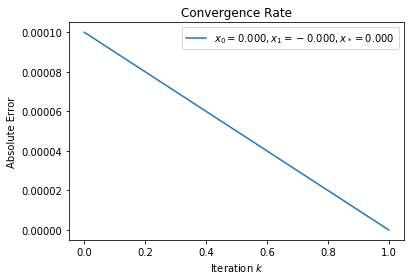
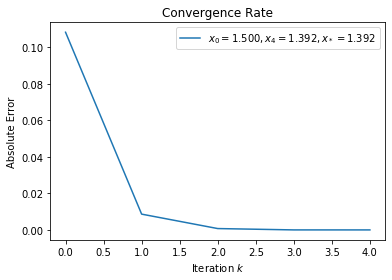
This formulation of Newton’s method will cycle when \(x_+ = -x_c\) such that
However, since Newton’s method was paired with backtracking, it will not cycle.
[13]:
hqn = HybridQuasiNewton()
f = lambda x: 2 * x - (1 + x * x) * numpy.math.atan(x)
x_0 = -1.5
x_star = -1.39174520382
solver = lambda x: hqn.evaluate_secant(f, x)
plot_convergent_sequence(solver, x_0, x_star)
x_0 = 0.0001
x_star = 0
plot_convergent_sequence(solver, x_0, x_star)
x_0 = 1.5
x_star = 1.39174520382
plot_convergent_sequence(solver, x_0, x_star)
[14]:
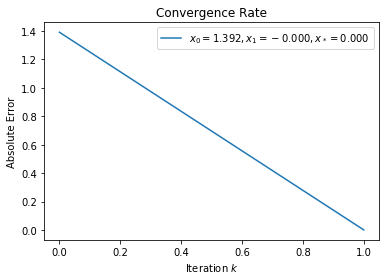
hqn = HybridQuasiNewton()
f = lambda x: numpy.math.atan(x)
x_0 = 1.39174520382
x_star = 0
solver = lambda x: hqn.evaluate_secant(f, x)
plot_convergent_sequence(solver, x_0, x_star)
Exercise 11¶
To minimize a one variable \(f(x)\), a quadratic model of \(f(x)\) around \(x_c\) is created and the critical point of the model is subsequently solved for.
One such quadratic model is the second-order Taylor series
such that
[15]:
import numpy
class NewtonQuadraticSolver1D:
def __init__(self, tau=None, typx=None):
self._kEpsilon = numpy.finfo(float).eps
self._kRootEpsilon = numpy.sqrt(self._kEpsilon)
#parameters to solver
self._tau = tau
if tau is None:
self._tau = (self._kRootEpsilon,) * 2
self._typx = typx
if typx is None:
self._typx = (1,)
def evaluate_newton(self, f, f_p1, f_p2, x_c):
denom = f_p2(x_c)
if denom > 0:
x_k = x_c - f_p1(x_c) / denom
else:
x_k = x_c + f_p1(x_c) / denom
x_n = self._backtracking_strategy(f, x_c, x_k)
return self._stop(f, f_p1, x_c, x_n), x_n
def _backtracking_strategy(self, f, x_c, x_n):
while f(x_n) >= f(x_c):
x_n = (x_c + x_n) / 2
return x_n
def _stop(self, f, f_prime, x_c, x_n):
return abs(f_prime(x_n) * x_n / f(x_n)) < self._tau[0] or\
abs(x_n - x_c) / max(abs(x_n), self._typx[0]) < self._tau[1]
[16]:
nqs1d = NewtonQuadraticSolver1D()
f = lambda x: x**4 + x**3
f_p1 = lambda x: 4 * x**3 + 3 * x**2
f_p2 = lambda x: 12 * x**2 + 6 * x
x_star = -0.75
x_0 = -0.1
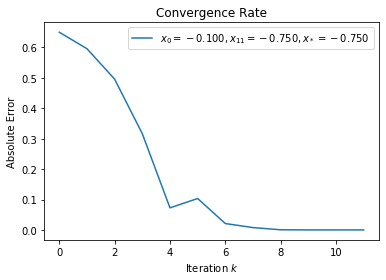
solver = lambda x: nqs1d.evaluate_newton(f, f_p1, f_p2, x)
plot_convergent_sequence(solver, x_0, x_star)
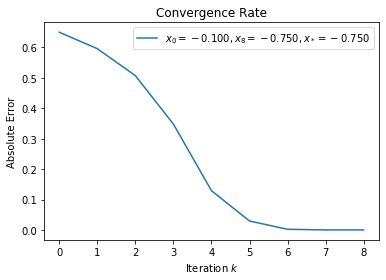
Exercise 12¶
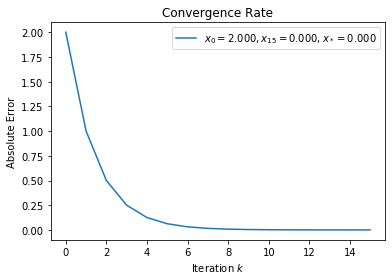
According to theorem 2.4.3, \(f(x) = x^2\) and \(f(x) = x^3\) converges q-linearly while \(f(x) = x + x^3\) and \(f(x) = x + x^4\) have q-quadratic convergence rate because \(f'(x_* = 0)\) must have a non-zero lower bound for Newton’s method to converge quadratically.
[17]:
hqn = HybridQuasiNewton()
f = lambda x: x**2
f_p1 = lambda x: 2 * x
x_star = 0
x_0 = 2
solver = lambda x: hqn.evaluate_newton(f, f_p1, x)
plot_convergent_sequence(solver, x_0, x_star)
[18]:
hqn = HybridQuasiNewton()
f = lambda x: x**3
f_p1 = lambda x: 3 * x**2
x_star = 0
x_0 = 2
solver = lambda x: hqn.evaluate_newton(f, f_p1, x)
plot_convergent_sequence(solver, x_0, x_star)
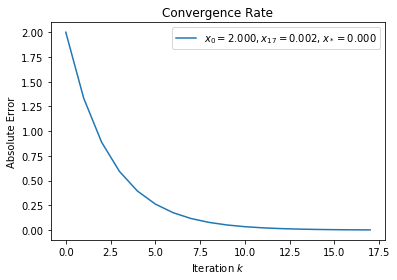
[19]:
hqn = HybridQuasiNewton()
f = lambda x: x + x**3
f_prime = lambda x: 1 + 3 * x**2
x_star = 0
x_0 = 2
solver = lambda x: hqn.evaluate_newton(f, f_prime, x)
plot_convergent_sequence(solver, x_0, x_star)
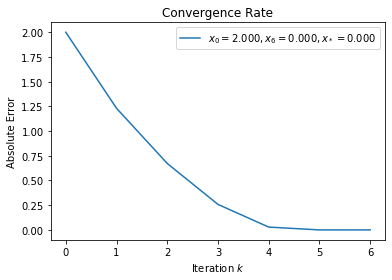
[20]:
hqn = HybridQuasiNewton()
f = lambda x: x + x**4
f_prime = lambda x: 1 + 4 * x**3
x_star = 0
x_0 = 2
solver = lambda x: hqn.evaluate_newton(f, f_prime, x)
plot_convergent_sequence(solver, x_0, x_star)
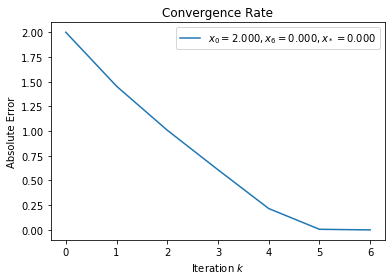
Exercise 13¶
Assume \(f(x)\) has \(n\) continuous derivatives on an interval about \(x = x_*\). \(f\) has a root (a.k.a. a zero) of multiplicity \(m\) at \(x_*\) if and only if
The foregoing implies \(f\) can be factorized as
where \(\lim_{x \to x_*} q(x) \neq 0\). Define \(e_{k + 1} = x_{k + 1} - x_*\) and \(e_k = x_k - x_*\). Newton’s method converges \(q\)-linearly to \(x_*\) because
Exercise 14¶
Assume \(f\) has \(n + 1\) continuous derivatives on an interval about \(x = x_*\) and satisfies
By inspection, \(f\) can be factorized as
where \(a \in \mathbb{R} \setminus \left\{ (x - x_*) \right\}\) and \(\lim_{x \to x_*} q(x) \neq 0\). Newton’s method converges \(q\)-cubicly to \(x_*\) because
where \(\rho, \gamma > 0\).
Exercise 15¶
An exact solution to the foregoing quadratic equation is
There are two (possibly three) major issues with this approach. The first is loss of significance due to the square root operation. The second is when \(f'(x_c)^2 \gg 2 f(x_c) f''(x_c)\) or \(f'(x_c)^2 \sim 2 f(x_c) f''(x_c)\). Lastly, \(x_k\) can be complex even if all the previous iterates were real.
A quadratic model is appropriate when the affine model is not satisfactory with respect to the desired criteria. It turns out this is equivalent to Halley’s irrational method [Ack].
Exercise 16¶
Assume \(f \in C^1(D)\), \(x_c \in D\), \(f(x_c) \neq 0\), \(f'(x_c) \neq 0\), and \(\mathrm{d} = -f(x_c) / f'(x_c)\).
Choose \(t\) such that \(f'(x_c + \lambda d) f'(x_c) > 0\) for all \(\lambda \in (0, t)\).
This illustrates that once the minimizing point \(x_*\) is almost reached using the suggested \(\mathrm{d}\) step size, the optimization can stop. However, this only works when the region has the same sign.
Exercise 17¶
will not be satisfied for \(f(x) = x^2\) because the relative error is constant (either 0.5 or 1.0) at each time step.
will be satisfied with an appropriately selected \(\text{typ}x\).
[21]:
f = lambda x: x**2
f_prime = lambda x: 2 * x
x_star = 0
x_c = 1
METHODS = ['Absolute Error',
'Current Value',
'Relative Error',
'Satisfy Condition']
STR_FMT = '{0!s:16}\t{1!s:16}\t{2!s:16}\t{3!s:16}'
print(STR_FMT.format(*METHODS))
typx = 1
SC = []
X_i = [x_c]
for i in range(0, 20):
x_k = Newtons_Method(f, f_prime, x_c)
x_c = x_k
X_i.append(x_k)
top = abs(X_i[i + 1] - X_i[i])
bot = max(abs(X_i[i + 1]), abs(typx))
print(STR_FMT.format(abs(x_k - x_star), f(x_k), top / bot,
(f(x_k) < 10e-5, top / bot < 10e-7)))
Absolute Error Current Value Relative Error Satisfy Condition
0.5 0.25 0.5 (False, False)
0.25 0.0625 0.25 (False, False)
0.125 0.015625 0.125 (False, False)
0.0625 0.00390625 0.0625 (False, False)
0.03125 0.0009765625 0.03125 (False, False)
0.015625 0.000244140625 0.015625 (False, False)
0.0078125 6.103515625e-05 0.0078125 (True, False)
0.00390625 1.52587890625e-05 0.00390625 (True, False)
0.001953125 3.814697265625e-06 0.001953125 (True, False)
0.0009765625 9.5367431640625e-07 0.0009765625 (True, False)
0.00048828125 2.384185791015625e-07 0.00048828125 (True, False)
0.000244140625 5.960464477539063e-08 0.000244140625 (True, False)
0.0001220703125 1.4901161193847656e-08 0.0001220703125 (True, False)
6.103515625e-05 3.725290298461914e-09 6.103515625e-05 (True, False)
3.0517578125e-05 9.313225746154785e-10 3.0517578125e-05 (True, False)
1.52587890625e-05 2.3283064365386963e-10 1.52587890625e-05 (True, False)
7.62939453125e-06 5.820766091346741e-11 7.62939453125e-06 (True, False)
3.814697265625e-06 1.4551915228366852e-11 3.814697265625e-06 (True, False)
1.9073486328125e-06 3.637978807091713e-12 1.9073486328125e-06 (True, False)
9.5367431640625e-07 9.094947017729282e-13 9.5367431640625e-07 (True, True)
Exercise 18¶
Choose \(\widehat{D} \subset D\) such that \(\left| f'(x) \right| \leq \alpha\) for all \(x \in \widehat{D}\) where \(\alpha > 0\).
Exercise 19¶
The following is one way of deriving the forward finite difference formula for first order derivative of \(f\) using Taylor expansion at \(x\):
Invoking Corollary 2.6.2 and the derivations in Exercise 20 gives
Assuming \(f(x_c + h_c) \cong f(x_c)\),
Note that if \(|f'(x)| \ll |f(x)|\), then the finite difference is going to evaluate to zero before ever reaching \(f'(x)\)’s vicinity because \(\text{fl}(f(x + h)) = \text{fl}(f(x))\).
Exercise 20¶
A couple useful facts to recall are
\(f'' \in \text{Lip}_\gamma(D)\) implies \(f''\) is continuously differentiable, which means \(f'''\) exists and is itself a continous function.
Any function can be written as \(f(z) \approx T_n(z) + R_n(z)\) where \(T_n(z)\) is the \(n\)-th degree Taylor polynomial of \(f\) at \(x\) and
\[R_n(z) = \frac{1}{n!} \int_x^z (z - t)^n f^{(n + 1)}(t) dt\]is the remainder of the series.
Weighted Mean Value Theorem for Integrals.
If \(f\) and \(g\) are continuous on \([a, b]\) and \(g\) does not change sign in \([a, b]\), then there exists \(c \in [a, b]\) such that
\[\int_a^b f(x) g(x) dx = f(c) \int_a^b g(x) dx.\]
Observe that when \(n = 2\) and \((z - t)^n\) does not change sign in the interval \([x, z]\),
A more rigorous proof would involve the Squeeze Theorem bounding \(R_n(z)\) as \(x \to z\) from the left and right side.
The following is one way of deriving the central difference formula for second order derivative of \(f\) using Taylor expansion at \(x\):
The following illustrates that the central difference formula has a tighter upper bound via invoking the previous derivations with \(z = x_c + h_c\) and \(x = x_c\).
Exercise 21¶
As demonstrated in Exercise 9, one approach is to compute the central finite difference for \(f''(x)\) using \(f'(x)\) and then apply the secant approximation to the forward finite difference for subsequent iterations.
[22]:
import numpy
class SecantQuadraticSolver1D:
def __init__(self, tau=None, typx=None):
self._kEpsilon = numpy.finfo(float).eps
self._kRootEpsilon = numpy.sqrt(self._kEpsilon)
#parameters to solver
self._tau = tau
if tau is None:
self._tau = (self._kRootEpsilon,) * 2
self._typx = typx
if typx is None:
self._typx = (1,)
self._secant_state = None
def evaluate_cfd(self, f, f_p1, x_c):
h_c = self._kRootEpsilon * max(abs(x_c), self._typx[0])
denom = (f_p1(x_c + h_c) - f_p1(x_c - h_c)) / (2 * h_c)
if denom > 0:
x_k = x_c - f_p1(x_c) / denom
else:
x_k = x_c + f_p1(x_c) / denom
x_n = self._backtracking_strategy(f, x_c, x_k)
return self._stop(f, f_p1, x_c, x_n), x_n
def evaluate(self, f, fp, x_c):
if self._secant_state is None:
#first iteration, so no previous results to use
h_c = self._kRootEpsilon * max(abs(x_c), self._typx[0])
#compute central finite difference
a_c = (fp(x_c + h_c) - fp(x_c - h_c)) / (2 * h_c)
#evaluate local model
fp_xc = fp(x_c)
if a_c > 0:
x_k = x_c - fp_xc / a_c
else:
x_k = x_c + fp_xc / a_c
self._secant_state = (x_c, fp_xc)
else:
#define h_c = x_previous - x_current
x_, fp_x_ = self._secant_state
#evaluate model with secant approximation
fp_xc = fp(x_c)
a_c = (fp_x_ - fp_xc) / (x_ - x_c)
if a_c > 0:
x_k = x_c - fp_xc / a_c
else:
x_k = x_c + fp_xc / a_c
self._secant_state = (x_c, fp_xc)
x_n = self._backtracking_strategy(f, x_c, x_k)
return self._stop(f, fp, x_c, x_n), x_k
def _backtracking_strategy(self, f, x_c, x_n):
f_xc = f(x_c)
while f(x_n) >= f_xc:
x_n = (x_c + x_n) / 2
return x_n
def _stop(self, f, f_prime, x_c, x_n):
return abs(f_prime(x_n) * x_n / f(x_n)) < self._tau[0] or\
abs(x_n - x_c) / max(abs(x_n), self._typx[0]) < self._tau[1]
[23]:
f = lambda x: x**4 + x**3
f_p1 = lambda x: 4 * x**3 + 3 * x**2
x_star = -0.75
x_0 = -0.1
sqs1d = SecantQuadraticSolver1D()
solver = lambda x: sqs1d.evaluate(f, f_p1, x)
plot_convergent_sequence(solver, x_0, x_star)
References
- Ack
Peter John Acklam. A small paper on halley’s method. http://web.archive.org/web/20151030212505/http://home.online.no/ pjacklam/notes/halley/halley.pdf. Accessed on 2017-01-28.
- Gay79
David M Gay. Some convergence properties of broyden’s method. SIAM Journal on Numerical Analysis, 16(4):623–630, 1979.
- Pot89
FA Potra. On q-order and r-order of convergence. Journal of Optimization Theory and Applications, 63(3):415–431, 1989.